РАЗРАБОТКА ВЫСОКОПРОИЗВОДИТЕЛЬНОГО МОНОКУЛЯРНОГО МЕТОДА ОЦЕНКИ 3Д-ПОЛОЖЕНИЙ ОБЪЕКТОВ НА ПРИМЕРЕ КЛАССА ОБЪЕКТОВ «АВТОМОБИЛЬ» АВТОНОМНОГО НАЗЕМНОГО ТРАНСПОРТА

Существуют различные методы, решающие задачу определения трехмерного положения объектов для автопилотируемого наземного транспорта для монокулярных изображений. К таковым можно отнести, например, Mono3D

В данной работе рассматривается новый метод, не применяющий регрессию положения через модифицированный выходной слой. Он использует комбинацию классического PnP-решателя и нейросети архитектуры YOLO новейшего поколения (YOLOv11s). Положение выявляется благодаря особому способу обучения нейросети, которая определяет не только сам объект, но и его ключевые визуальные особенности, благодаря чему метод решения PnP определяет конечное положение без дополнительной вычислительной нагрузки на видеоускоритель. Это позволяет достичь значительного (до 10–20 раз) улучшения производительности по сравнению с классическими для этой задачи методами глубокого обучения.

Система использует калибровочные параметры камеры и априорные знания о геометрии типовых объектов. Предлагаемая архитектура системы включает следующие последовательные этапы обработки:

1. Двумерная детекция объектов: Обнаружение объектов на входном изображении и получение их двумерных ограничивающих рамок и классов с помощью предобученной нейросетевой модели. На этом этапе также могут быть детектированы характерные части объектов, используемые для уточнения.

2. Оценка трехмерного положения опорной точки объекта: Определение начальной трехмерной точки, ассоциированной с объектом, путем сопоставления его двумерной детекции с характерными признаками и последующей проекции на предполагаемую опорную плоскость.

3. Оптимизация ориентации объекта: Итерационное уточнение угла поворота объекта вокруг вертикальной оси путем минимизации ошибки между проекцией его трехмерной модели и наблюдаемыми двумерными признаками.

Входными данными для системы служат: монокулярное RGB-изображение, внутренние и внешние параметры калибровки камеры (калибровочная матрица ), аппроксимирующие 3D боксы для объектов по умолчанию.

Выходными данными являются: трехмерные координаты центра объекта в системе координат камеры. Угол ориентации объекта относительно оси камеры.

Использование гибридных моделей также позволяет получать сегментированную поверхность дороги, дорожные знаки и другую полезную информацию без снижения скорости работы. Общая схема представлена на рис. 1.

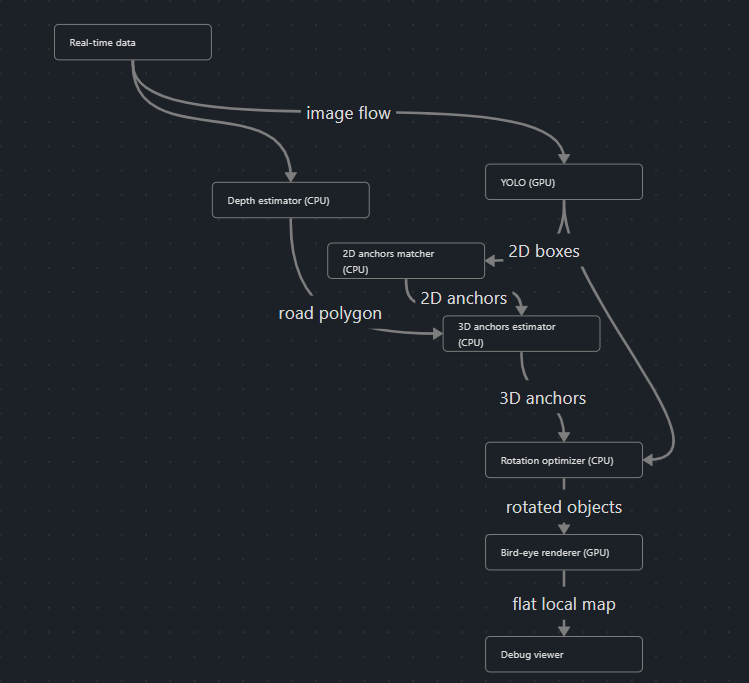
Рисунок 1 - Общая схема разработанного метода

DOI:10.60797/COMP.2025.7.2.1

Система является логическим развитием представленной в работе

[3]

.

2.1. Основные понятия, термины

Якорь 2D — опорная точка на изображении, которая отвечает положению обнаруженного объекта, привязана к земле. Является отправной для построения якоря 3D.

Якорь 3D — опорная точка в трехмерном пространстве, соответствующая положению объекта на поверхности, по которой он перемещается. Является отправной точкой для построения канонической 3D модели объекта методом решения PnP.

Каноническая 3D модель — габариты объекта выбранного класса.

Тень бокса 3D объекта - проекция канонической 3D модели объекта на плоскость XY мировых координат сцены. Фактически отражает точность положения объекта на плоской карте.

2.2. Модуль двумерной детекции объектов и их характерных признаков

Первичным этапом работы системы является обнаружение объектов на входном изображении. Для этой цели была применена сверточная нейронная сеть, обученная на задачу детекции объектов. Была выбрана YOLOv11s (small), как модель, обеспечивающая достаточную кадровую частоту на GTX1650 (30-35 кадров в секунду) с сохранением приемлемой точности. Более крупные модели (medium, large) уже не способны обеспечить достаточную кадровую частоту. В сравнении с предыдущим поколением демонстрирует прирост точности вместе с улучшением быстродействия. На данный момент является самой продвинутой среди YOLO-моделей с официальной реализацией от Ultralitycs. Выбранная нейронная сеть была дообучена на наборе классов «car», «car_rear», «car_front» для получения необходимых данных для дальнейшей работы алгоритма. Каждый основной класс требует дообучения для классов-признаков, поэтому в работе приводится один.

Модель принимает на вход изображение и возвращает набор двумерных ограничивающих рамок для каждого обнаруженного объекта, а также соответствующий ему класс («car» — «Автомобиль») и оценку уверенности.

Помимо детекции основного объекта, система может использовать детекции его характерных частей или признаков («car_front», «car_rear» — «передняя часть автомобиля», «задняя часть автомобиля»). Эти вспомогательные детекции получаются либо той же нейросетью (если она обучена на множественные классы), либо отдельной специализированной моделью. Наличие таких признаков позволяет определить якори для последующей 3D-оценки.

После получения двумерных детекций следующим шагом является определение начального трехмерного положения для каждого объекта.

Для каждого основного детектированного объекта (например, «Автомобиль») система ищет наиболее подходящий характерный признак (например, «передняя часть автомобиля» или «задняя часть автомобиля») из числа обнаруженных на предыдущем этапе. Сопоставление производится на основе правила, учитывающего геометрическую близость и взаимное расположение рамок основного объекта и его признаков.

В результате сопоставления для основного объекта выбирается одна из точек на его 2D-рамке (или рамке признака), которая будет служить 2D-якорем (опорной точкой) . Эта точка соответствует определенной, заранее известной локальной точке  на канонической 3D-модели объекта (например, центр нижней грани задней части автомобиля). Выбор конкретной  зависит от того, какой признак был сопоставлен и какая часть этого признака была выбрана в качестве .

2.3. Модуль определения 3D координат опорной точки

Зная 2D-координаты опорной точки на изображении и калибровочную матрицу камеры P, можно построить луч в трехмерном пространстве, исходящий из оптического центра камеры и проходящий через эту точку. Направление этого луча в системе координат камеры можно получить из уравнения (1)

(1)

Разрешая это уравнение относительно при условии, что точка лежит на луче, и нормализуя, получаем вектор направления. Точнее, если — матрица внутренних параметров камеры (, где для простоты можно считать, что камера находится в начале координат и ее оптическая ось совпадает с осью , т.е. , для получения луча в системе координат камеры), то направление луча можно найти как:

(2)

Затем этот луч нормализуется: .

Оптический центр камеры (в ее собственной системе координат) обычно принимается за .

Далее, предполагается, что выбранная опорная точка объекта (например, точка на уровне колес) лежит на известной опорной плоскости (например, дорожном полотне). Эта плоскость задается своей нормалью и точкой на плоскости (например, точка под камерой на высоте дороги). Трехмерные координаты  искомой опорной точки объекта находятся как точка пересечения луча  с этой плоскостью

(3)

где параметр находится из уравнения плоскости (3)

(4)

При этом проверяется, что пересечение происходит перед камерой () и знаменатель не слишком близок к нулю (луч не параллелен плоскости).

2.4. Модуль оптимизации ориентации объекта

После получения начальной оценки 3D-положения опорной точки и зная соответствующую ей локальную точку на 3D-модели, следующим шагом является определение ориентации объекта, в частности, угла поворота вокруг вертикальной оси.

Оптимизация ориентации формулируется как задача минимизации функции ошибки (невязки) , которая характеризует степень несоответствия между проекцией 3D-модели объекта (повернутой на угол ) на изображение и наблюдаемыми 2D-признаками (например, границами исходной 2D-рамки объекта).

(5)

В качестве функции ошибки может использоваться сумма квадратов разностей между горизонтальными координатами (-координатами) краев исходной 2D-рамки объекта и проекциями соответствующих пар вершин 3D-модели объекта, которые должны соответствовать этим краям при оптимальном :

(6)

где и — это целевые -координаты на изображении (например, левая и правая границы исходной 2D рамки объекта, или -координаты проекций диагональных точек, которые должны соответствовать определенным частям 2D рамки).

Для вычисления функции ошибки на каждой итерации оптимизации выполняются следующие шаги:

Построение канонической 3D-модели: Используются априорные средние размеры объекта (длина , ширина , высота ) для определения координат его 8 вершин в локальной системе координат объекта, где якорь лежит на оптимизируемой диагонали.

Локальный поворот модели: Вершины локальной модели центрируются относительно локальной опорной точки (которая использовалась на этапе 2.3), поворачиваются вокруг вертикальной оси на текущий угол с помощью матрицы поворота , а затем смещаются обратно:

(7)

Глобальное размещение модели: Повернутые локальные вершины переносятся в глобальную систему координат камеры. Это достигается путем такого смещения, чтобы локальная опорная точка (после поворота, если она не центр вращения) совпала с ранее оцененной глобальной 3D-опорной точкой . Если была центром вращения, то повернутые вершины смещаются так, чтобы их новый центр (бывший ) оказался в . Более точно, если , то , и

Проекция на изображение. Мировые координаты вершин  проецируются на плоскость изображения с использованием полной калибровочной матрицы :

(8)

Из этих проекций  выбираются необходимые координаты (например, ) для вычисления функции ошибки.

Для минимизации функции ошибки используется итерационный численный метод. В данной работе рассматривается применение метода Гаусса-Ньютона (или аналогичного квазиньютоновского метода), который хорошо подходит для задач минимизации суммы квадратов невязок.

Итерационный процесс продолжается до выполнения одного из критериев остановки. Достигнуто максимальное заданное число итераций. Изменение значения функции ошибки или параметра между последовательными итерациями становится меньше заданного малого порога . После выполнения оптимизации на выходе имеем сориентированные в пространстве канонические 3D модели объектов на виртуальной сцене.

Для оценки эффективности были применены две конфигурации тестов. Первая конфигурация включала в себя оценку по неизменной плоскости дороги. Вторая предполагала, что есть точное значение глубины у пикселя якоря. Использовался стандартный оценочный скрипт на C++, поставляемый официально вместе с датасетом. Он также строит графики Precision-Recall для каждой оцениваемой характеристики.

3.1. Набор данных

Все экспериментальные исследования проводятся на широко используемом в задачах автономного вождения наборе данных KITTI, в частности, на его подвыборке для 3D-детекции объектов. Он содержит синхронизированные данные с различных сенсоров, включая монокулярные камеры, лидар, а также точную разметку трехмерных ограничивающих рамок для объектов на изображениях из обучающей выборки (training set). Для работы метода использовались изображения из левой цветной камеры и соответствующие файлы калибровки, содержащие матрицу проекции . Поскольку нейросеть была дообучена для определения положения объектов класса «автомобиль», именно он и был выбран для проверки эффективности метода. Для оценки использовался полный набор, содержащий 7480 изображений.

3.2. Метрики оценки качества

Для количественной оценки производительности предлагаемой системы используются следующие метрики, стандартные для задачи 3D-детекции объектов на датасете KITTI:

Точность 3D-локализации:

1. Сравнение проекций на плоскость (BEV IoU / тени на землю).

Двумерная оценка перекрытия реализуется посредством проекции 3D-боксов на горизонтальную плоскость — это планарная аппроксимация объекта. Оценивается IoU в Bird’s Eye View.

2. Точность оценки ориентации.

Метрика Average Orientation Similarity (AOS) из протокола KITTI, которая учитывает как точность 2D-детекции, так и ошибку ориентации для (AOS применяется только к тем объектам, для которых выполнено условие перекрытия (IoU) с истинным объектом в 2D-пространстве).

3. Средняя точность.

Average Precision (AP): Средняя точность, вычисленная для различных порогов 3D IoU (стандартная — 0.7 для KITTI) и для разных категорий сложности объектов (Easy, Moderate, Hard), как определено в официальном протоколе оценки KITTI.

Кроме качества будем оценивать скорость обработки данных, а также сравним полученные показатели с другими монокулярными методами.

Первый график — оценка ошибки для трехмерной ориентации бокса по оси  (рис. 2). 

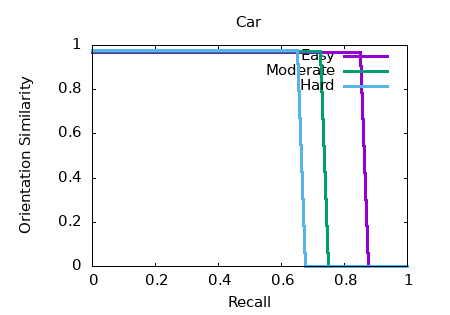
Рисунок 2 - График оценки mAp для 3D-ориентации

DOI:10.60797/COMP.2025.7.2.2

Как видно из графика, оценка достаточно точно отражает реальный поворот автомобиля по соответствующей оси. Итоговая точность на классе «car» составляет: 

Easy: mAP AOS ≈ 82,49.

Moderate: mAP AOS ≈ 71,27.

Hard: mAP AOS ≈ 64,38.

Для сравнения в таблице 1 представлены другие методы и их показатели.

Представленные результаты говорят о несильном отставании от передовых методов, при этом скорость обработки выше в разы, что можно видеть в таблице 2.

Несмотря на высокую производительность и точность 3D ориентации, без хорошей аппроксимации глубины в точках установки якоря он не демонстрирует большую точность 3D позиционирования (рис. 3).

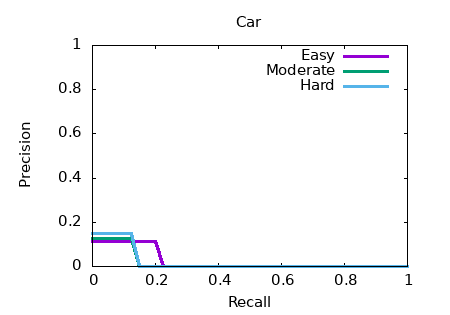
Рисунок 3 - Показатели точности совпадения силуэтов для аппроксимации глубины плоскостью

DOI:10.60797/COMP.2025.7.2.5

Однако при сопоставлении построении глубины сторонними методами, точность значительно возрастает (рис. 4).

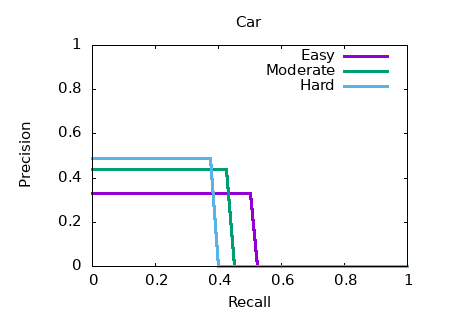
Рисунок 4 - Точность аппроксимации теней 3D-боксов при уточнении глубины

DOI:10.60797/COMP.2025.7.2.6

Данные показывают, что точность возрастает до значений:

Easy: mAP BEV ≈ 17,02.

Moderate: mAP BEV ≈ 19,27.

Hard: mAP BEV ≈ 19,09.

Сравнивая с другими методами, метод демонстрирует наиболее высокую точность на сложных участках, неплохую на средних и наиболее низкую на легких. Связан такой результат с тем, что методу необходимо видеть объект в кадре полностью, чтобы его аппроксимировать по одному изображению.

Таким образом, показатели становятся сравнимыми с другими методами, при том, что точность более равномерно распределена между сложными и простыми случаями. Результат работы - рис. 5.

Рисунок 5 - Пример работы алгоритма

DOI:10.60797/COMP.2025.7.2.8

В представленном методе впервые показано, что предварительная сегментация дороги и последующая быстрая аппроксимация её плоскости позволяют получить конкурентоспособную точность 3D‑оценки и ориентации без явного восстановления полной глубины сцены. Основные выводы и преимущества метода:

4.1. Сбалансированное соотношение «точность — скорость»

Средний BEV mAP на уровнях Easy/Moderate/Hard составляет 17,02% / 19,27% / 19,09%, что близко к результатам передовых монокулярных методов (SMOKE, OPA‑3D, DID‑M3D), особенно в сложных сценах (Hard).

Ориентационная метрика (orientation AOS) на уровне Easy ≈ 82,5%, Moderate ≈ 66,5%, Hard ≈ 59,6% — лишь слегка уступает SMOKE и другим методам, при этом скорость обработки достигает 25–33 FPS на GTX 1650 Mobile, что в 1,5–2,5× быстрее SMOKE и в 4–6× быстрее RTM3D.

4.2. Встроенная сегментация дороги

Пайплайн на основе нейросетей архитектуры YOLO (ее производных seg-сетей) позволяет выполнять не только детекцию объектов, но и сегментацию дороги, что позволяет избежать отдельного модуля сегментации и снизить вычислительную нагрузку.

Сегментационные данные можно использовать для обнаружения доступной для проезда части поверхности (отделяя пешеходную часть, бордюры, перепады высоты, глубокие ямы), и занося ее в смоделированную сцену.

Наличие сегментной маски может быть использовано для дальнейшего уточнения геометрии, например, RANSAC‑аппроксимации плоскости дороги

4.3. Ограничения приближённой плоскости

Простая аппроксимация плоскостью может быть полезна в контролируемой среде, например на складе или заводе. В этом случае методы аппроксимации поверхности, по которой едет объект не нужно и это упрощает вычисления. Для применения в реальности необходимо построение разреженной или плотной карты глубины. При этом оно может происходить параллельно, и не в реальном времени, а в режиме «непрерывной дорисовки». Также построение карты глубины можно совместить с локализацией в подобие SLAM-метода

4.4. Фундаментальные ограничения и их обход

Метод имеет фундаментальное ограничение, из-за которого он должен видеть признаки объекта в кадре, чтобы строить модель габаритов. Также, чтобы строить верную модель габаритов, в текущей реализации еще нужно, чтобы сам объект бы полностью видим на изображении. Если алгоритм работает с системой всенаправленных камер, они незначительны. Но даже если существуют слепые пятна, можно улучшить реализацию и добиться хорошей точности даже на не полностью видимых объектах. Первое ограничение нивелируется увеличением количества признаков так, чтобы любая небольшая часть объекта обладала своим. Второе ограничение (даже без наращивания числа признаков) можно обойти, аппроксимируя угол поворота не по двум границам 2D бокса, а по одной, полностью видимой. Видимость можно определять по касанию 2D рамок бокса границ изображения. Также можно, например, помечать неожиданно появляющиеся на виртуальной сцене объекты как «ненадежные», но по мере их существования в зоне видимости увеличивать коэффициент надежности (так как работа ведется с видеопотоком). Это позволит трассирующему маршрут методу уделять особое внимание областям с «ненадежными» объектами.

4.5. Возможные направления улучшения

Учёт углов камеры: интеграция IMU данных или онлайн‑оценка кренов/тангажа для компенсации ориентации камеры перед проекцией.

Дополнительные классы габаритов объектов: Для улучшения точности 3D-аппроксимации можно обучить нейросеть таким образом, чтобы разбивать автомобили по классу габаритов, и сопоставлять им соответствующие 3D-боксы. Сейчас всем автомобилям соответствует один стандартный бокс, что не мешает методу верно аппроксимировать поворот, но не габариты теней боксов.

Лёгкая «глубокая коррекция»: добавление мини‑глубинной ветви (несколько сверточных слоев), обученной на исправление ошибок плоской аппроксимации, без значительного замедления.

Предложенный метод показывает, что простая и быстрая аппроксимация дорожной плоскости на основе единой маски позволяет достигать сопоставимой с современными монокулярными подходами точности 3D-оценки и ориентации при значительном выигрыше по скорости. Его преимущества:

Ключевое преимущество — производительность: 20–33 FPS на мобильной GTX 1650 при сохранении mAP BEV и AOS на конкурентном уровне.

Интеграция сегментации и детекции: отсутствие отдельного модуля сегментации дороги упрощает пайплайн и снижает накладные расходы.

Простота доработок: метод легко дополняется локальной коррекцией плоскости и учётом углов камеры для повышения точности.

В целом, комбинирование эффективного детектора YOLOv11s и упрощённой геометрической модели сцены открывает перспективы применения в системах реального времени и ограниченных устройствах. Дальнейшая работа будет ориентирована на гибридные решения, объединяющие скорость аппроксимации и точность локальных коррекций.