APPLICATION OF THE THEORY OF OPTIMAL CONTROL FOR THE DEVELOPMENT OF AN EXPERT SYSTEM OF PROFESSIONAL EDUCATION

Моделирование и управление процессом обучения в общем случае является крайне нетривиальной задачей ввиду сложности протекания совокупных процессов организма человека, которые следует рассматривать в разрезе ряда отраслей естественнонаучного познания. Мозг человека содержит около 100 миллиардов нейронов, которые объединяются в нейронные ансамбли.

Каждому приобретенному образу памяти (слову, предмету, явлению) соответствует свой нейронный ансамбль. Нейроны ансамбля, хранящие один образ, активизируются согласованно, циклически. Колебания клеточных потенциалов, связанные с импульсацией нейронов, создают повторяющийся узор биопотенциалов. Причем каждому образу соответствует свой собственный узор. Часть нейронов ансамбля могут «замолкать» или включаться в работу другого ансамбля, другого образа. При этом ансамбль может не только приобретать нейроны (повторение), но и терять их (забывание). Предполагается, что работу одного ансамбля может обеспечить число нейронов от 100 до 1000

Единичный ансамбль сам по себе не может стать основой сознания. Однако мы можем представить сценарий, согласно которому отдельные ансамбли возникают независимо. Правда, к тому времени как их активность естественным образом угасает, она, а точнее ее энергия, переносится в некий коллективный пул (метаансамбль). Энергия должна быть сохранена в некоторой химической, электрической или тепловой форме. В какой бы форме ни осуществлялась эта крупномасштабная передача энергии, она будет ощутимо влиять на фоновую активность мозга. Эта неравномерная, волнообразная активность чрезвычайно чувствительна к искажениям и способна порождать глобальные всплески, которые могут оказаться реальным и окончательным коррелятом момента сознания. Мы должны предусмотреть форму интеграции крупномасштабных, пространственно ограниченных нейронных коалиций, которые могут возникать в пределах временного окна продолжительностью в несколько сотен миллисекунд, то есть в виде своего рода нейронного «пространственно-временного многообразия». Поскольку многообразие является математическим понятием, которое объединяет пространство и время в едином континууме, рассматривая время как четвертое измерение, нейронный метаансамбль будет описан в конечном итоге скорее физиками-теоретиками, чем нейробиологами

При этом каждый нейрон связан со множеством других нейронов нейронно-синаптическими связями. Есть надежда, что при таком колоссальном количестве нейронно-синаптических связей на уровне целого организма, появляются новые свойства, присущие средним величинам.

Если обратиться к истории науки, то можно увидеть, как одни и те же результаты могли быть получены разными методами и подходами. Ярким примером может быть сравнение термодинамики и статистической физики. Исторически сложилось, что термодинамика появилась намного раньше статистической физики.

Предмет статистической физики, составляет изучение особого типа закономерностей, которым подчиняются поведение и свойства тел макроскопических, т. е. тел, состоящих из колоссального количества отдельных частиц-атомов и молекул. Статистические – закономерности, обусловленные именно наличием большого числа составляющих тело частиц, ни в какой степени не могут быть сведены к чисто механическим закономерностям. Таким образом, хотя движение систем с огромным числом степеней свободы подчиняется тем же законам механики, что и движение систем из небольшого числа частиц, наличие большого числа степеней свободы приводит к качественно новым закономерностям

Можно привести аналогии между поведением нейронов в метаансамбле и описанием средних величин для всего организма, приведя преемственность между термодинамикой и статистической физикой. Дадим прогноз будущего развития нейрологии с математическим описанием процессов обучения, сравнив переход от термодинамики к статистической физике.

Результаты, приведенные в данной статье, отражают информационный подход на основе феноменологических данных психологии и педагогики, одновременно основываясь на фундаментальных теориях современного естествознания.

Для создания полноценной экспертной системы обучения требуется разработать математическую модель обучения на основе теории управления, в котором управление присутствует в явном виде. Далее следует аналитически решить задачу оптимального управления процессом обучения. При этом экспертная система должна строить персональную траекторию обучения на основе численного решения задачи оптимального управления процессом обучения.

С достаточной точностью можно аппроксимировать экспериментальные данные, установленные Эббингаузом

(1)

где − текущий уровень (объем) усвоенного учебного материала (в академических часах),

 − начальный уровень усвоенного учебного материала при ,

 − коэффициент забывания, который показывает, какую часть от текущего уровня усвоенного учебного материала  обучаемый забывает в среднем за сутки.

Считая время непрерывным, продифференцируем (1) по времени  и получим однородное линейное дифференциальное уравнение, представляющее свободное движение системы:

(2)

Уравнение (2) имеет достаточно простой физический смысл − это процесс постепенного забывания, отталкиваясь от некоторых начальных условий. Начальный уровень уже усвоенного учебного материала обозначим как .

Получим теперь неоднородное линейное дифференциальное уравнение как сумму свободного и вынужденного движений системы:

(3)

где  − функция мощности внешнего информационного источника, которая характеризует информационное воздействие на обучаемого (в академических часах) за время .

Решение уравнения (3) представляется следующей формулой:

(4)

Правая часть уравнения (4) представляет собой сумму свободной и вынужденной компонент процесса обучения. Представим внешнюю компоненту процесса обучения в виде управления учебной нагрузкой, которая подается в определенные промежутки времени.

В технических системах функцию управления разбивают на два вида: программное и с обратной связью

Представим учебную нагрузку  в виде суммы:

,

где  – программное управление, задаваемое в виде заранее запланированной учебной нагрузки, осуществляемой преподавателем традиционным способом в аудитории (в академических часах),

 – программное управление, осуществляемое преподавателем онлайн,

 – программное управление в виде нагрузки для самостоятельного обучения,

 – программное управление посредством видеолекций.

Реальный процесс обучения обязательно включает в себя повторение уже изученного материала (управление с обратной связью). Таким образом, добавляя еще четыре вида управлений с обратной связью объем усвоенных знаний из (3) можно составить из восьми частей:

(5)

где  – управление процессом повторения посредством контрольных и самостоятельных работ после обучения преподавателем традиционным способом в аудитории,

 – управление процессом повторения после обучения преподавателем онлайн,

 – управление процессом повторения материала после самостоятельного обучения,

 – управление процессом повторения после обучения с помощью видеолекций,

 − коэффициент усвоения для управления .

Пределы изменения всех коэффициентов: (, , ). Все коэффициенты можно определить с помощью специальных тестов.

Таким образом, процесс обучения можно описать с помощью неоднородного линейного дифференциального уравнения

(6)

решение которого можно представить в виде

(7)

Управление в реальном процессе обучения является кусочно-непрерывным.

Кривые обучения для разных коэффициентов забывания и усвоения при кусочно-непрерывном равномерном программном управлении представлены на рисунках (рис. 1, рис. 2.)

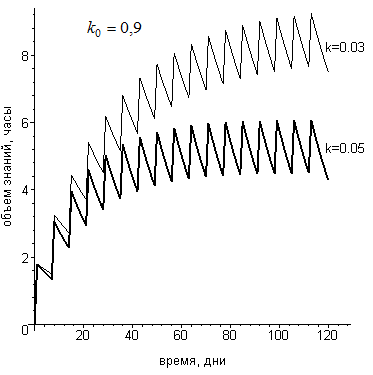
Рисунок 1 - Кривые обучения для разных коэффициентов забывания

Примечание: k0=0,9

DOI:10.18454/COMP.2024.1.1.1

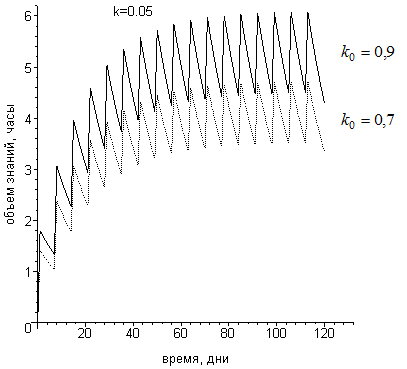
Рисунок 2 - Кривые обучения для разных коэффициентов усвоения k0

Примечание: k=0,05

DOI:10.18454/COMP.2024.1.1.2

Проведем аппроксимацию нижней кривой на рисунке 2. с помощью полинома (рис. 3):

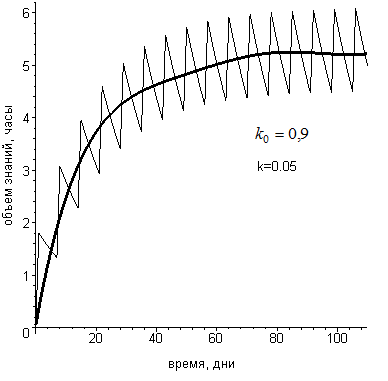
Рисунок 3 - Аппроксимированная кривая обучения

Примечание: k0=0,9, k=0,05

DOI:10.18454/COMP.2024.1.1.3

Из рисунков 1, 2, 3 видно, что форма кривой обучения для непрерывного программного управления, полученных на основе математической модели (6), аналогична феноменологической классической кривой научения, описанной в источнике

[6]

, представленной на рисунке (рис. 4). Таким образом, при любой равномерной нагрузке теоретически получается классическая кривая научения.

Рисунок 4 - Классическая кривая научения

DOI:10.18454/COMP.2024.1.1.4

У человека существует «кратковременная» и «долговременная» память, характеризуемые различными временами запоминания и хранения информации

[7]

.

Кратковременная память обеспечивает удержание ограниченной части поступившей информации, позволяет воспроизводить какую-то ее часть и тем самым некоторое время использовать определенное количество информации.

Долговременная память позволяет сохранять информацию неограниченное время и имеет практически неограниченный объем, сохраняет огромное количество информации без искажения. Информация при необходимости может легко воспроизводиться

Процесс, происходящий при обработке информации в кратковременной памяти, является затухающим процессом. В долговременной памяти в основном фиксируются события, значимые для организма. Долговременная память сама по себе, вне момента ее образования и извлечения, представляется не процессом, а структурой (с многоуровневым пространственным распределением). В этом причина ее устойчивости к многочисленным внешним воздействиям, и в этом ее существенное отличие от сенсорной и кратковременной форм памяти, которые, по сути, являются процессами

Для устойчивого запоминания в процессе обучения необходимо обеспечить переход знаний у обучаемых из кратковременной памяти в долговременную. Это достигается путем повторения учебного материала. Данный процесс можно описать с помощью математического моделирования с постепенным убыванием значения коэффициента забывания  по следующей формуле

(8)

где  − коэффициент забывания для некоторого объема усвоенного учебного материала, который был повторен  раз.

В источнике

(9)

Все коэффициенты усвоения стремятся к единице при достаточно большом числе повторений.

Для практического применения математической модели (6) необходимо провести аналитические и численные расчеты для двух видов оптимального управления (программного и с обратной связью), разработать экспертную систему обучения, которая обеспечит оптимальный режим повторения учебного материала с целью максимального уменьшения коэффициента забывания и увеличения восьми коэффициентов усвоения.

При обычной организации учебного процесса программные управления  планируются заранее и являются кусочно-непрерывными. Траектории обучения, представленые на рисунках 1 и 2 демонстрируют, что при данных «хороших» коэффициентах усвоения и забывания, обучаемый усваивает к концу семестра только 4-8 академических часов из 34 часов, данных при программном управлении.

Таким образом, обучаемый может усвоить нужный объем учебного материала при первом изучении только в том случае, если он имеет очень высокие коэффициенты усвоения (близкие к единице) и очень низкий коэффициент забывания (близкий к нулю).

Во всех остальных случаях требуется подключать управление с обратной связью в виде повторения ранее изученного учебного материала. Реальный учебный процесс должен быть построен с помощью оптимального режима повторения учебного материала.

Задача оптимального управления с обратной связью сводится к нахождению оптимальных управлений с обратной связью  (синтез оптимального регулятора).

Имеем исходное дифференциальное уравнение изучаемого процесса (в случае обучения с помощью преподавателя)

(10)

Рассмотрим функционал качества управления обучением

(11)

Функционал (11) имеет значение на интервале . Разобьем (11) на два слагаемых

,

где  – функционал потерь, который минимизируется, обеспечивая минимальную учебную нагрузку при повторении всего учебного материала:

 – функционал качества обучения, который характеризует сохранение усвоенного объема знаний за счет улучшения коэффициентов забывания и усвоения. Этот функционал представляет подынтегральную площадь, которую формирует траектория обучения  на временном интервале :

,

Достаточным условием минимума функционала (11) является уравнение Беллмана для непрерывных детерминированных систем

(12)

с граничным условием

(13)

и управление , удовлетворяющее условию

(14)

с ограничением

(15)

то  является оптимальным управлением с полной обратной связью,

где  – максимально допустимый объем повторенной учебной нагрузки.

Уравнение Беллмана (12) и уравнение (10) линейны по , поэтому оптимальное управление  с ограничением (15) будет релейным

,

которое удовлетворяет условию (14).

Тогда оптимальное управление с обратной связью

(16)

Из системы (16) при граничном условии (13) можно определить условие включения режима поворения

.

Пусть требуется определить оптимальную траекторию обучения с закрепленными концами (из точки  в точку , где ). В качестве функции  можно взять в первом приближении опорную траекторию в виде прямой, соединяющую начальную и конечную точки.

.

Тогда режим оптимального повторения учебного материала определяется формулой:

(17)

где  – управление с обратной связью, построенное на основе теории оптимального управления,

 – объем повторенного учебного материала для момента времени  из материала, данного преподавателем в аудитории.

Общий повторенный объем определяется с помощью суммы:

где  – число контрольных и самостоятельных работ на повторение пройденного материала,

 – полный объем учебного курса.

Оптимальная траектория обучения рассчитывается по формуле

(18)

На основе математической модели обучения, метода оптимального управления с обратной связью создан прототип экспертной системы обучения (ПЭСО). Прототип разработан на языке программирования C# в среде разработки Visual Studio.

Рассмотрим, какими будут оптимальное режим повторения учебного материала и оптимальная траектория обучения с использованием ПЭСО при разных параметрах ().

Пусть учебное расписание задано так: равномерное изучение нового учебного материала один раз в неделю по 2 часа в течение 17 недель (всего – 34 часа). На рисунке 5 представлена траектория обучения для оптимального управления с обратной связью при коэффициентах усвоения ,  и коэффициенте забывания , построенная по формуле (18). В качестве опорной траектории взята прямая, проведенная от начала координат до точки , где  день на 17-й неделе обучения,  составляет 50% от общей нагрузки по предмету при программном управлении. В нижней консоли окна ПЭСПО описаны рекомендации по оптимальному повторению учебного материала.

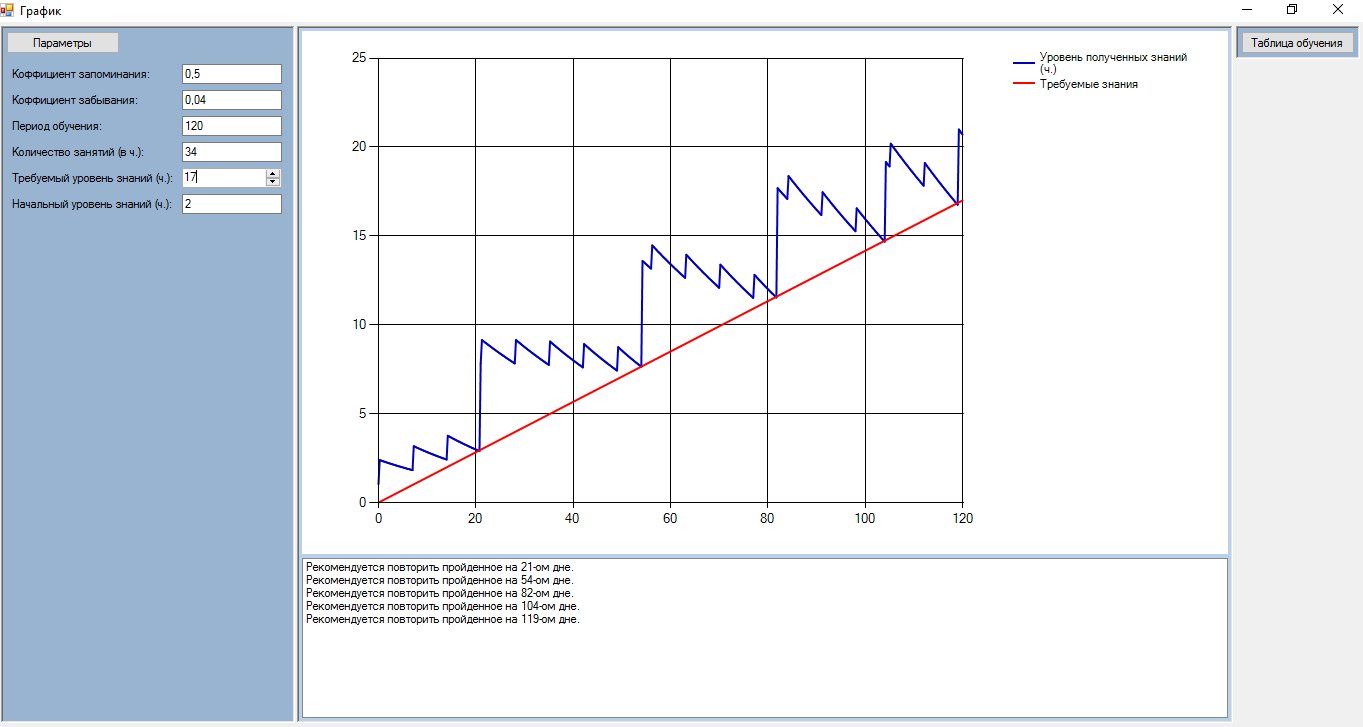
Рисунок 5 - Траектория обучения для оптимального управления с обратной связью

DOI:10.18454/COMP.2024.1.1.5

В данной работе описана математическая модель обучения в виде линейного дифференциального уравнения (6). Для решения задачи оптимального управления с обратной связью выписано уравнение Беллмана в частных производных и найдено соответствующее оптимальное управление с обратной связью (16), дающее минимум функционала качества (11). На основе математического метода управления с обратной связью процессом обучения разработан прототип экспертной системы обучения на языке программирования C# в среде разработки Visual Studio, в котором были строятся кривые обучения для программного управления и управления с обратной связью для различных коэффициентов усвоения и забывания. На основе прототипа экспертной системы обучения со временем может быть создана полноценная экспертная система обучения.