A MATHEMATICAL MODEL OF THE DIGITAL SYSTEM OF AUTOMATIC TARGET TRACKING BY RANGE WITH THE USE OF THE "CODE-TIME DELAY" SCHEME

Как показывает анализ работы современной авиационной техники, ее эксплуатация осуществляется при широком воздействии разнообразных параметров (радиопомех, маневра целей и прочее). Эффективность работы воздушного судна во многом определяется системой автоматического сопровождения цели. Особенно это относится к работе систем автоматического сопровождения целей по угловым координатам и дальности (АСД). Запаса динамической устойчивости и быстродействия не всегда хватает для устойчивого автоматического сопровождения маневренных целей, что приводит к бесконтрольному режиму управления. При этом существенно повышаются и ошибки сопровождения целей

В данной статье была разработана математическая модель цифровой системы автоматического сопровождения цели для обеспечения эффективности и безопасности полётов маневренных целей.

Преобразователь код-временная задержка (ПКЗ) и генератор селектирующих импульсов (GІ) являются формирователем управляющих по задержке импульсов. В каждом такте работы ПКЗ осуществляется преобразование числа NK(kT) в пропорциональный ему временной сдвиг выходного импульса. Принцип работы ПКЗ объясняется на рис. 1.

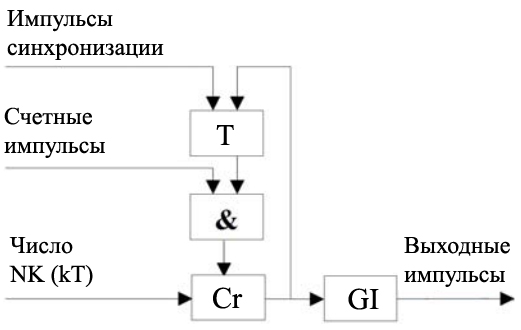
Рисунок 1 - Структурная схема преобразователя «код-временная задержка»

DOI:10.18454/COMP.2024.2.1.1

Начало следующего такта работы определяет нахождение на вход триггера Т синхронизирующих импульсов.

При этом происходит опрокидывание триггера Т и напряжение на его выходе увеличивается. В результате счетные импульсы через схему «&» начинают поступать на счетчик импульсов Cr. В счетчик предварительно записывается с обратным знаком число NK (kT). После поступления в счетчик NK счетных импульсов в нем фиксируется число ноль, а на выходе появляется импульс переполнения, который используется для запуска генератора селектирующих импульсов. Одновременно выходной импульс ПКЗ возвращает триггер Т в исходное состояние

Преобразователь код-временная задержка и генератор импульсов являются практически безынерционными устройствами

(1)

Структура математической модели преобразователя «код – временная задержка» приведена на рис. 2.

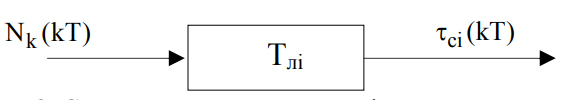
Рисунок 2 - Структура математической модели преобразователя «код-временная задержка»‎

‎

DOI:10.18454/COMP.2024.2.1.2

2.1. Построение математической модели преобразователя «код-временная задержка»

Преобразователь код-временная задержка (ПКЗ) и генератор селектирующих импульсов (GІ) являются формирователем управляющих по задержке импульсов. В каждом такте работы ПКЗ осуществляется преобразование числа NK(kT) в пропорциональный ему временной сдвиг выходного импульса. Принцип работы ПКЗ объясняется на рис. 1.Начало следующего такта работы определяет нахождение на вход триггера Т синхронизирующих импульсов.

При этом происходит опрокидывание триггера Т и напряжение на его выходе увеличивается. В результате счетные импульсы через схему «&» начинают поступать на счетчик импульсов Cr. В счетчик предварительно записывается с обратным знаком число NK (kT). После поступления в счетчик NK счетных импульсов в нем фиксируется число ноль, а на выходе появляется импульс переполнения, который используется для запуска генератора селектирующих импульсов. Одновременно выходной импульс ПКЗ возвращает триггер Т в исходное состояние

Преобразователь код-временная задержка и генератор импульсов являются практически безынерционными устройствами

(1)

Структура математической модели преобразователя «код – временная задержка» приведена на рис. 2.

2.2. Анализ устойчивости системы АСД

Для анализа устойчивости цифровой системы АСД необходимо определить характеристический многочлен замкнутой системы. Для этого необходимо определить оператор передачи разомкнутой схемы автоматического управления (САУ) R(S).

Как следует из рис.3, 

(2)

где:

R(S) – оператор передачи разомкнутой схемы автоматического управления (САУ),

K0 (S) – линейный стационарный разностный оператор оценивания дальности,

Ke (S) – линейный стационарный разностный оператор экстраполяции дальности,

Kgr – коэффициент усиления с размерностью (одиночный разряд), связывающий величину погрешности дальности, выраженную в метрах, со значением исходного кода ПНК.

После подстановки K0(S) получаем:

(3)

где q=kgr/km – отношение фактической крутизны дискриминаторной характеристики к ее значению, хранящемуся в преобразователе код-временная задержка и цифровом код-преобразователе (0<q<1).

Для определения условий устойчивости схемы автоматического управления составим характеристическое уравнение:

(4)

Для того чтобы система была устойчивой, корни данного уравнения должны быть по модулю меньше единицы. Поэтому дальнейшее решение задачи сводится к отысканию корней Z1 и Z2 и определению областей значений параметров K1 и K2T, при которых Z2 <1 и Z1<1.

Более просто эта задача может быть решена с использованием критерия устойчивости Гурвица. Для этого преобразуем характеристический многочлен C(Z) в многочлен:

C(ν) = (1 — ν)n C(Z), Z = 1 + ν / 1 — ν

где ν – комплексная переменная, имеющая положительную часть при Z<1

(5)

Согласно критерию устойчивости Гурвица, для того чтобы схема автоматического управления второго порядка была устойчива, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительными

2К1 + К2Т < V,

K1 > 0,

K2T > 0.

Область устойчивости можно изобразить графически (рис. 3).

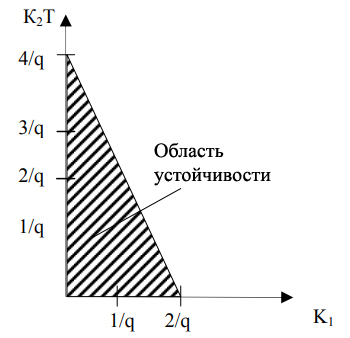
Рисунок 3 - Область устойчивости цифровой системы АСД

DOI:10.18454/COMP.2024.2.1.3

Для оценки показателей качества системы автоматического сопровождения дальности в переходном режиме используем прямой метод, потому что система автоматического сопровождения дальности имеет второй порядок астатизма и для нее не сложно определить переходную характеристику H(nT).

Z – изображение переходной характеристики H (nT) имеет вид:

Раскладывая на дроби выражение для H (Z), получим следующий результат:

(6)

Конечное выражение для переходной характеристики зависит от характера корней знаменателя второй дроби. Первой дроби соответствует единичная ступенчатая решетка функции 1(nT – T).

В общем виде переходную характеристику можно записать в следующем образе:

(7)

Если корни знаменателя второй дроби выражения (6) комплексно сопряжены, тогда функции h1(nT) s h2 (nT) выражаются через умножение гармонической и показательной решетчатой функции

График переходной характеристики системы АСД показан на рис. 4.

2.3. Оптимизация параметров Ки и К2 алгоритма оценивания и экстраполяции по критерию минимума среднеквадратичной погрешности

Согласно условиям задачи, ввиду воздействия-дискретный белый шум с дисперсией Df, а влияние-детерминированная функция вида:

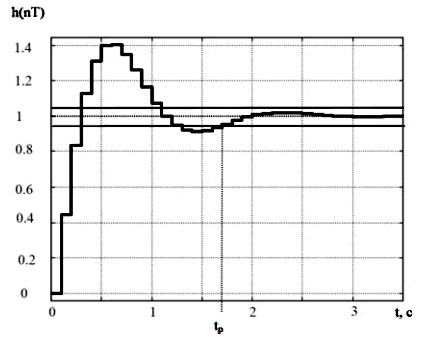
Рисунок 4 - Переходная характеристика системы АСД

DOI:10.18454/COMP.2024.2.1.4

Среднеквадратичная погрешность сопровождения определяется следующим образом:

Используя метод коэффициентов погрешностей, определим математическое ожидание динамической погрешности сопровождения

Следовательно, квадрат среднеквадратичной ошибки равно:

Как видим, отдельные составляющие среднеквадратичной погрешности различным образом зависит от K2T: первая составляющая обратного квадрата K1T, а вторая монотонно увеличивается с увеличением K2T. Второе приложение по изменению K1 имеет минимум, который имеет способ решения.

При аналитическом решении задачи необходимо определить производные d(S2)/d(K2T) і d(S2)/d(K1), и, сравнив их с нулем, отыскать из полученных уравнений значения K2T и K1, поставляют экстремум функции K2T, а затем выбрать те значения K2T и K1, при которых обеспечивается минимум среднеквадратичной погрешности.

При аналитическом решении задачи необходимо определить производные d(S2)/d(K2T) и d(S2)/d (K1), и, сравнив их с нулем, отыскать из полученных уравнений значения K2T и K1, получаем экстремум функции K2T, а затем выбрать те значения K2T и K1, при которых обеспечивается минимум среднеквадратичной погрешности.

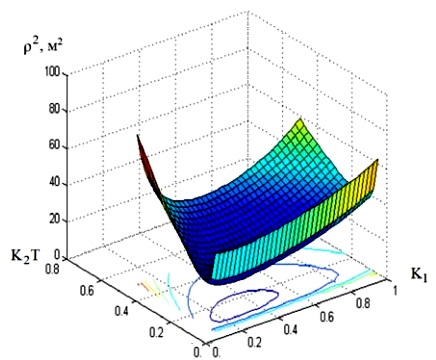
Рисунок 5 - Зависимость среднего квадрата ошибки р2 от параметров алгоритма K1 и K2T

DOI:10.18454/COMP.2024.2.1.5

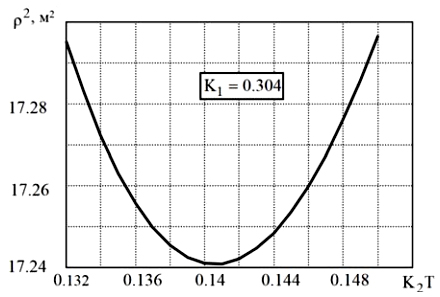
Рисунок 6 - Зависимость среднего квадрата ошибки р2 от параметра K2T при K1 =0.304

DOI:10.18454/COMP.2024.2.1.6

Из последнего уравнения получаем выражение для оптимального параметра, удовлетворяющего условию K1 устойчивости, в виде функции от параметра K2T:

(8)

Если это выражение для K1 подставить в уравнение K1 (8), получим уравнение для определения оптимального значения параметров в виде функции K2T от дисперсии эквивалентного влияния, которое мешает Df и ускорение g, которое можно решить в числовой форме.

График зависимости р2 от K1 и K2T приведен на рис. 5. А если выражение подставить в уравнение K1 (8), тогда график зависимости р2 от K2T будет иметь вид, который приведен на рис. 6. Таким образом, оптимальное значение K2T=0,141, а K1=0,304.

Лучше разрабатывать системы на цифровой элементной базе и делать оптимизацию систем, исходя из критериев оптимизации, выбрать параметры систем, которые разрабатываются. Для этого необходимо иметь цифровые модели соответствующих систем сопровождения целей. Хотя аналоговая система автоматического сопровождения дальности (АСД) характеризуется простотой конструктивного исполнения, но в то же время им свойственны такие недостатки, как относительно невысокая стабильность параметров, дрейфы нулей операционных усилителей, необходимость постоянных регламентных работ в процессе эксплуатации. В этом отношении цифровые системы АСД отличаются в лучшую сторону. У этих систем высокая стабильность параметров, которая не зависит от воздействия внешней среды

На основании исследования модели системы автоматического сопровождения дальности проведен анализ устойчивости и качества системы. Определены допустимые области параметров алгоритма работы цифрового управляющего устройства, при которых система автоматического сопровождения дальности соответствует своему предназначению. Также рассчитаны систематические и флуктуационные погрешности, оптимизированные параметры алгоритма и по критерию минимума средне-K1 K2 квадратичной погрешности, оценены инструментальные погрешности и сопоставления по флуктуационной погрешности. При выборе параметров системы, по условиям ее устойчивости, когда K2T=0,141 и K1=0,304, возможно К2Т K1 обеспечить погрешность определения дальности, которая не превышает 10 м. На основании проведенного анализа качества системы автоматического сопровождения дальности выбрана оценка младшего разряда в преобразователе напряжение-код. Выбирая цену наименьшего разряда преобразователя напряжение-код менее 0,23 в, можно не учесть влияние инструментальных погрешностей, которые обусловлены квантованием по уровню в преобразователе напряжение-код, влияющий на качество работы системы автоматического сопровождения дальности. Таким образом, по результатам моделирования были обеспечении требования к показателям устойчивости и качества системы автоматического сопровождения дальности, что вполне удовлетворяют требованиям к таким системам.