The use of digital technologies in the Mathematics-1 course to increase the effectiveness of adaptation for preparatory course students
The use of digital technologies in the Mathematics-1 course to increase the effectiveness of adaptation for preparatory course students
Abstract
The article examines the use of digital technologies in the Mathematics-1 course to prepare applicants for university-level mathematics. The main objective of the study is to identify the effect of interactive tools on student performance, adaptation, and satisfaction. The research was conducted on the basis of preparatory courses with two groups: a control group (traditional teaching) and an experimental group (using digital technologies, including Moodle, GeoGebra, Desmos, and online testing). The results showed that the implementation of digital tools contributes to a significant increase in student performance, adaptation and satisfaction. Methods for integrating digital technologies into the Mathematics-1 course are presented, the results of the experiment are analysed, and recommendations for the further development of the course are given.
1. Введение
Современные тенденции развития образования характеризуются активной цифровизацией и переходом к новым форматам взаимодействия между преподавателем и обучающимися. В условиях роста объёма информации и распространения дистанционных форм обучения всё большее значение приобретает формирование у будущих студентов навыков самостоятельной аналитической работы, цифровой компетентности и критического мышления.
Курс Mathematics-1, реализуемый в рамках подготовительных программ Инженерно-технологического университета Туркменистана, выполняет важную адаптационную функцию: он формирует базовые математические компетенции, необходимые для успешного освоения университетских дисциплин, таких как линейная алгебра, математический анализ и дискретная математика.
Актуальность темы исследования определяется необходимостью повышения эффективности обучения абитуриентов, испытывающих трудности при переходе от школьной к академической математике. Внедрение цифровых инструментов в курс Mathematics-1 позволяет сделать процесс обучения более интерактивным, гибким и индивидуализированным.
Новизна исследования заключается в системной оценке влияния цифровых технологий на адаптацию слушателей подготовительных курсов. Если ранее подобные подходы применялись преимущественно в школьной или вузовской среде , , то в данной работе цифровизация рассматривается как инструмент именно предвузовской подготовки. Практическая значимость состоит в возможности тиражирования предложенной модели в других образовательных учреждениях и её интеграции в гибридные форматы обучения.
Цель исследования — оценить эффективность внедрения цифровых технологий в курс Mathematics-1 как средства адаптации слушателей к университетскому обучению.
Для достижения цели поставлены следующие задачи:
1) проанализировать цифровые инструменты, применяемые в курсе;
2) провести педагогический мини-эксперимент для выявления их влияния на успеваемость и адаптацию;
3) определить уровень удовлетворённости слушателей применяемыми средствами;
4) разработать рекомендации по развитию цифрового контента курса.
2. Теоретические основы применения цифровых технологий
Цифровизация образовательного процесса открывает широкие возможности для повышения эффективности преподавания и совершенствования учебных коммуникаций. В курсе Mathematics-1 используются платформы Moodle и Google Classroom для организации учебного контента и мониторинга прогресса, приложения GeoGebra и Desmos для визуализации графиков и геометрических построений, а также системы компьютерной алгебры (CAS) и онлайн-тестирования для контроля знаний.
Использование цифровых средств способствует повышению вовлечённости и снижает стресс при изучении академической математики. A.H. Brown и T.D. Green отмечают, что эффективность технологий проявляется не только в передаче знаний, но и в развитии самостоятельности обучающихся и способности к саморегуляции.
Кроме того, цифровые среды обеспечивают более наглядное представление абстрактных математических понятий, повышая мотивацию и вовлечённость. Интерактивные симуляции и динамические модели позволяют студентам экспериментировать с параметрами задач, тем самым углубляя понимание закономерностей. Это особенно важно на подготовительном этапе, когда формируется фундамент математического мышления.
3. Методы исследования
Для оценки эффективности цифровых технологий был проведён педагогический эксперимент на базе подготовительных курсов при университете. В нём участвовали две группы по 25 человек: контрольная, с традиционным обучением, и экспериментальная, с использованием цифровых инструментов (Moodle, GeoGebra, Desmos, онлайн-тестирование). Продолжительность эксперимента составила один семестр.
Учебные материалы были структурированы в соответствии с принципами модульного обучения. Каждая тема сопровождалась цифровыми ресурсами: видео-лекциями, интерактивными заданиями и тестами различного уровня сложности. Преподаватели использовали элементы обратной связи, включая онлайн-консультации и автоматизированный анализ ошибок.
Для количественной оценки эффективности использовались следующие показатели:
– средний прирост успеваемости (Δ), определяемый по формуле
где S1 средний балл до внедрения цифровых технологий, S2 — средний балл после внедрения цифровых технологий;
– уровень адаптации (по результатам анкетирования);
– уровень удовлетворённости цифровыми инструментами.
Итоговое тестирование и анкетирование позволили сопоставить результаты и выявить влияние цифровой среды на когнитивные и мотивационные аспекты обучения.
Для оценки эффективности применения цифровых технологий в курсе Mathematics-1 был проведён педагогический эксперимент на базе подготовительных курсов при университете. В исследовании приняли участие две группы слушателей по 25 человек каждая: контрольная (традиционное обучение) и экспериментальная (с использованием цифровых инструментов). Продолжительность эксперимента — один семестр. В конце обучения проводилось итоговое тестирование и анкетирование слушателей для оценки уровня адаптации и удовлетворённости цифровыми средствами обучения (см. табл. 1).
Таблица 1 - Результаты эксперимента по курсу Mathematics-1
Показатель | Контрольная группа | Экспериментальная группа |
Средний балл (до) | 64,0 | 63,0 |
Средний балл (после) | 68,0 | 78,0 |
Прирост, % | 6,25 | 23,8 |
Уровень адаптации, % | 72,0 | 91,0 |
Удовлетворённость цифровыми инструментами, % | 65,0 | 89,0 |
Результаты визуализированы на рисунках 1–3. На рисунке 1 представлена динамика успеваемости, на рисунке 2 — уровень адаптации, на рисунке 3 — удовлетворённость цифровыми инструментами. Все графики показывают заметное улучшение показателей в экспериментальной группе по сравнению с контрольной.
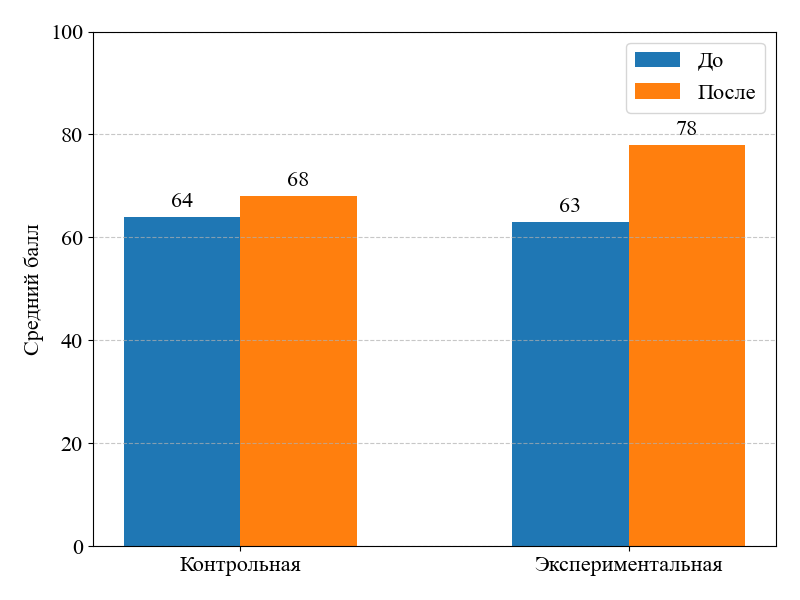
Рисунок 1 - Динамика успеваемости по курсу Mathematics-1
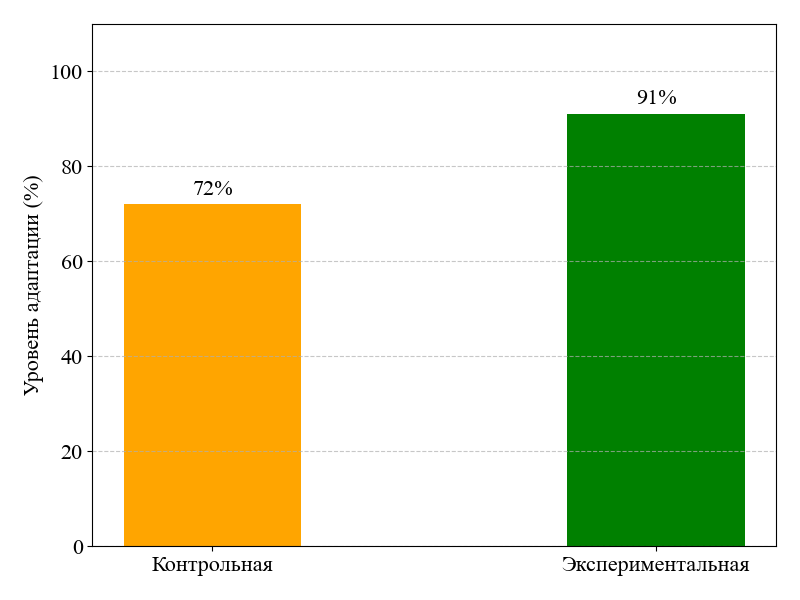
Рисунок 2 - Уровень адаптации слушателей
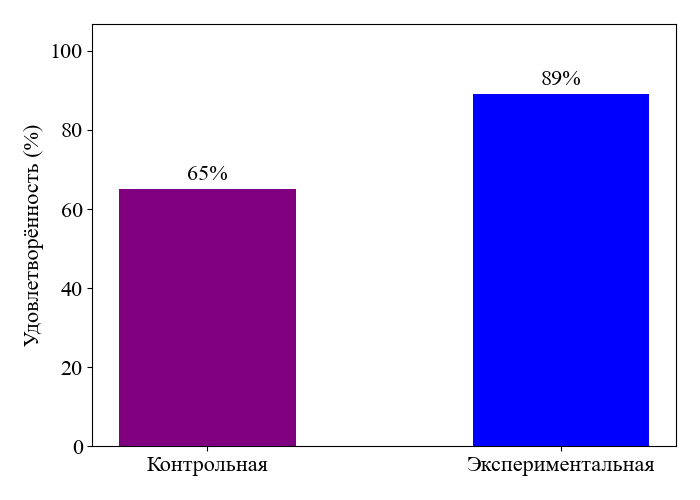
Рисунок 3 - Удовлетворённость цифровыми инструментами
Прирост успеваемости в экспериментальной группе на 23,8% свидетельствует о высокой результативности цифровых методов. D.W. Johnson и R.T. Johnson установили, что элементы интерактивного обучения усиливают групповую динамику и развивают навыки сотрудничества, что также наблюдалось в данном исследовании.
Кроме того, выявлено, что цифровые технологии способствуют снижению тревожности при изучении сложных тем, так как позволяют обучающимся самостоятельно регулировать темп и глубину усвоения материала. Рост уровня адаптации на 19 п.п. и удовлетворённости до 89% подтверждает эффективность цифровой среды как инструмента психологической поддержки и повышения уверенности.
Перспективным направлением развития курса является создание интерактивных модулей по темам «Предел», «Функции нескольких переменных» и «Основы линейной алгебры». Также планируется внедрение адаптивных систем тестирования, элементов геймификации и интеграция цифровых ресурсов с дистанционными платформами для формирования индивидуальных образовательных траекторий .
4. Заключение
Проведённое исследование показало, что использование цифровых технологий в курсе Mathematics-1 способствует значительному повышению эффективности обучения и адаптации слушателей. Интеграция онлайн-платформ, интерактивных сред и систем компьютерного тестирования позволяет индивидуализировать процесс обучения, повысить мотивацию и развить цифровые компетенции.
Результаты мини-эксперимента подтвердили, что цифровые технологии повышают успеваемость на 17,5 п.п., уровень адаптации — на 19 п.п., а удовлетворённость слушателей достигает 89%. Таким образом, цифровизация курса Mathematics-1 может рассматриваться как один из ключевых инструментов успешной адаптации абитуриентов к университетской математике и основа дальнейшего развития гибридных форм обучения.
